Toková křivka polymerních tavenin neboli viskozitní křivka (závislost smykového napětí na rychlosti smykové deformace v log-log měřítku) mají dvě odlišné chování, které popisuje Newtonuv a Mocninův zákon. Při velmi nízkých smykových rychlostech dominuje newtonovské chování, kde je viskozita nezávislá na rychlosti smykové deformace a přibližuje se hodnotě, která byla pojmenována jako viskozita s nulovou rychlostí. Poté se viskozita začne snižovat při určité kritické smykové rychlosti (y0). Při vyšších smykových rychlostech dominuje chování podle mocenského zákona, kde viskozita klesá se zvyšující se rychlostí smykové deformace se záporným sklonem (n-1). Parametr n byl pojmenován jako index newtonského chování.
Toková křivka polymerních tavenin neboli viskozitní křivka (závislost smykového napětí na rychlosti smykové deformace v log-log měřítku) mají dvě odlišné chování, které popisuje Newtonuv a Mocninův zákon. Při velmi nízkých smykových rychlostech dominuje newtonovské chování, kde je viskozita nezávislá na rychlosti smykové deformace a přibližuje se hodnotě, která byla pojmenována jako viskozita s nulovou rychlostí. Poté se viskozita začne snižovat při určité kritické smykové rychlosti (y0). Při vyšších smykových rychlostech dominuje chování podle mocenského zákona, kde viskozita klesá se zvyšující se rychlostí smykové deformace se záporným sklonem (n-1). Parametr n byl pojmenován jako index newtonského chování.
.jpg)
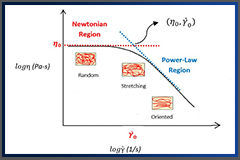
Obrázek 1: Typická toková křivka polymerní taveniny
Jak je vidět na obrázku 1, je toková křivka polymerních tavenin vázána dvěma omezujícími sloty (přerušované čáry), které určují hodnotu viskozity s nulovým rychlostí smykové deformace (n00 a hodnotu indexu newtonského chování (n)). Používá se k výpočtu molekulové hmotnosti (Mw) a šířky distribuce molekulové hmotnosti (MWD). Teplota, tlak, aditiva, plniva a lubrikanty jsou dalšími faktory, které mohou mít vliv na tvar křivky viskozita/smyková rychlost.
Existuje několik kvantitativních vztahů, které představují závislost rychlosti smykové deformace a viskozity polymerních materiálů, jako je model mocninova zákona, Bird-Carreau-Yasuda model, Crossův model a Cross-WLF model. Model mocninového zákona je níže znázorněn jako rovnice:
kde k je index konzistence (Pa-s) a n je index newtonského chování. Typicky mají polymerní taveniny hodnotu n v rozmezí 0,2 až 0,6 v závislosti na typu polymeru a jeho chemické struktuře. Model Mocninova zákona vyhovuje pouze křivkové části (Power law) a je to užitečný pro řízení procesu. Avšak oblast newtonské části křivky nelze takto popsat. Obvykle data z kapilárního reometru spadají do oblasti smykového napětí a lze je dokonale přizpůsobit pomocí modelu Mocninova zákona. Obrázek 2 ukazuje analýzu přizpůsobení modelu mocninova zákona (pomocí softwaru LabKars) na dvou druzích polyethylenu (PE) materiálů pomocí kapilárního reometru Dynisco LCR7001.
Obrázek 2. Analýza a použítí mocninového zákona
Crossův model byl vyjádřen jako rovnice níže:
Smyková viskozita (Pa-s), kde t je kritické smykové napětí (Pa) nebo napětí při přerušení křivky a je indexem Power-Law. Obrázek 3 ukazuje modifikovanou analýzu křížového modelu (ze softwaru LabKars) na dvou typech PE materiálů pomocí kapilárního reometru Dynisco LCR7001.
Figure 3. Analýza a použítí Crossova modelu
Tento model kombinuje Mocninlův zákon a newtonské oblasti a představuje úplnější popis tokové křivky. Je to užitečný model pro zachycení hodnoty viskozity s nulovým napětím.
Zdroj čerpání:
- J.M. Dealy, and K.F. Wissbrun, Melt Rheology and its Role in Plastics Processing: Theory and Applications, Van Nostrand Reinhold, New York (1990).
- C.L. Rohn, Analytical Polymer Rheology, Hanser (1995).


.JPG)
.jpg)
.JPG)
.jpg)